“Thửa”, “ô”, “lô”, “mảnh” là các khái niệm cơ bản trong hình thái học đô thị. Thiết kế hệ thống giao thông kết hợp với phân chia đất theo dạng “thửa”, “ô”, “lô”, “mảnh” là một hoạt động cơ bản của công tác quy hoạch, đưa vùng quy hoạch trở thành một cấu trúc dạng tổ hợp có sự liên kết và phân cấp. Cấu trúc này có nhiều điểm tương đồng với các tổ hợp hình học Fractal- dạng hình học non trẻ nhất, sáng lập bởi nhà toán học Mandelbrot. Kể từ khi ra đời vào thập niên 70, hình học Fractal đã được biết đến là “hình học của tự nhiên” nhờ khả năng mô tả các cấu trúc phức tạp mà hình học truyền thống Euclid không thực hiện được và nhanh chóng lan tỏa trong tất cả mọi lĩnh vực bao gồm cả kiến trúc xây dựng nói chung. Bài báo này khái quát các khái niệm về hình thái thửa – ô – lô mảnh trong quy hoạch đô thị, kiến thức cơ bản về tạo hình tổ hợp trong hình học Fractal và đánh giá khả năng ứng dụng tạo hình các tổ hợp Fractal trong nghiên cứu quy hoạch thửa – ô – lô mảnh và hình thái đô thị nói chung.
Một số khái niệm cơ bản về hình thái thửa – ô – lô, mảnh
Thửa: Những diện tích đất được phân chia và bao bọc bởi các tuyến đường giao thông, có thể thấy rõ trên các bản đồ quy hoạch 1/25 000, 1/10 000 hay 1/5000. Hình 1.1 minh họa cấu trúc phân chia ô thửa của TP Florence (Italia). Các tuyến đường xác định các cấu trúc kẻ ô và tán xạ. Từ đó các ô mảnh có hình thái đa dạng được hình thành.
Ô phố: Là một quần thể của các lô, mảnh được giới hạn bởi các tuyến đường phố có mối quan hệ với cấu trúc quy hoạch dưới góc độ phân chia đất đai. Hình thái các ô phố chịu tác động bởi cấu trúc đường phố. Chúng có vị trí quan trọng trong việc tạo ra các thửa, ô, lô mảnh. Và ngược lại, các thửa, ô, lô mảnh cũng tác động tới sự hình thành cấu trúc đường phố.
Ô phố là một yếu tố hình thái của đô thị, nằm trong mối quan hệ tay ba giữa cấu trúc đường phố, thửa và lô mảnh. Phân chia không gian trong ô phố, đó là sự phân chia không gian đô thị theo sở hữu và đưa vào đó các chức năng xây dựng. Mỗi ô sẽ có từ hai trở lên các mảnh có công trình xây dựng. Việc phân chia không gian trong ô phố sẽ tạo ra những lô mảnh chịu tác động bởi những tuyến đường phố cũ hoặc mới. Chính những tuyến đường này sẽ tạo nên một cấu trúc với sự hình thành những thửa hoặc ô khác nhau. Hình 1.2 minh họa một số dạng hình thái ô phố.
Lô, mảnh: Là một dạng của hình thức quy hoạch. Phân lô không phải là một phép cộng đơn giản các lô mảnh để lấp đầy khoảng trống. Người ta có thể điều chỉnh thêm vào một cách chừng mực những lô mảnh dọc theo các tuyến phố để tạo nên hình thái đa dạng của ô. Như vậy ô là một tập hợp của các lô mảnh có giới hạn của một thửa đất và được tạo nên bởi đường phố. Hình 1.3 minh họa một số kiểu phân chia lô, mảnh trong ô phố.
Một số lí thuyết cơ bản về tổ hợp hình học Fractal
Khái niệm tổ hợp hình học Fractal
Tổ hợp hình học Fractal hay Fractals (trong tiếng Anh): Là khái niệm trừu tượng trong toán học dùng để mô tả các sự vật tổ hợp từ nhiều phần nhỏ, hình thành một cách tự nhiên, có hình dạng gấp khúc trên mọi tỷ lệ phóng đại. Trong đó, mỗi phần nhỏ hơn lại tương tự hoặc giống như tổng thể hoặc phân đoạn lớn hơn chứa phần đó. Như vậy, mỗi tổ hợp hình học Fractal “có vô tận các chi tiết, các chi tiết này có thể có cấu trúc tự đồng dạng ở các tỷ lệ phóng đại khác nhau. Nhiều trường hợp, có thể tạo ra tổ hợp Fractal bằng việc lặp lại một mẫu toán học, theo phép hồi quy. Có thể phân các tổ hợp hình học Fractal thành Fractal toán học và Fractal tự nhiên”, [1,3,8]
Quy luật tạo hình của hình học Fractal
Có nhiều cách thức để tạo hình Fractal trong đồ họa. Về cơ bản, chúng đều phải áp dụng tính chất tự đồng dạng [14] theo kiểu đệ quy: Lặp đi lặp lại một quá trình với mức độ nhỏ dần đều.
Phương pháp tư duy đơn giản nhất đó là tư duy hình khởi tạo – hình phát sinh [1, 13].
- Hình khởi tạo – Initiator: Hình khởi tạo hay đối tượng ban đầu để tạo hình Fractal được gọi là Initiator. Đó có thể là một đoạn thẳng, một đa giác hay một đường cong (hình tròn, ellip,…) và có thể là một đối tượng bất kỳ trong tự nhiên.
- Hình phát sinh – Generator: Một tập hợp được sắp hết từ những hình đồng dạng của yếu tố khởi tạo (đoạn thẳng, đa giác…) được sử dụng để thay thế Initiator nhằm tạo nên hình Fractal mong muốn được gọi là một Generator.
- Mức – Level: Khi Initiator được thay thế bởi Generator, ta có “hình Fractal mức 1”. “Hình Fractal mức 1” này trở thành tập hợp Initiator với tỷ lệ nhỏ hơn và lại được thay thế bởi các Generator, ta được “hình Fractal mức 2”….Như vậy, có thể hiểu mức của hình Fractal là số lần lặp lại việc thay thế Intiator bởi các Generator (Hình 2.2).
Để khiến cho hình ảnh mang tính chất tự nhiên, người ta có thể bổ sung thêm 1 biến thể ngẫu nhiên nào đó trong các bước. Ví dụ Hình 2.3.
Ngày nay, quy luật tạo hình Fractal và các biến thể ngẫu nhiên được kết hợp với lập trình đồ họa để tạo ra những hình ảnh nghệ thuật trừu tượng phức tạp hoặc những hình ảnh mô phỏng tự nhiên như thật. Hình 2.4 là một số ví dụ hình ảnh trừu tượng và mô phỏng tự nhiên được tạo ra nhờ thuật toán Fractal ứng dụng trong lập trình đồ họa máy tính.
Đánh giá khả năng ứng dụng hình học Fractal trong nghiên cứu quy hoạch thửa – ô – lô, mảnh dựa trên sự tương đồng về tạo hình
Hình học Fractal được biết đến nhiều nhất bởi nguyên tắc tạo hình đặc biệt. Giữa hình thái đô thị với dạng thức quy hoạch kiểu thửa – ô – lô, mảnh và các tổ hợp hình học Fractal có nhiều điểm tương đồng, cụ thể như sau:
Đều là những tổ hợp có hình dạng phức tạp:
Hình thái đô thị được tạo nên từ các tuyến giao thông lớn nhỏ đan xen cùng các thửa, ô, lô, mảnh đất trong lớn hàm chứa nhỏ, nhiều nhỏ hợp lại thành lớn. Do tính chất tự phát trong mỗi quá trình phát triển đô thị, ranh giới mỗi đô thị không phải là một đường trơn nhẵn mà gồ ghề, zich zắc. Cấu trúc bên trong mỗi đô thị cũng phân chia hết sức phức tạp do ảnh hưởng của các vấn đề văn hóa, xã hội, tập quán của cư dân. Vì thế, không thể dùng hình vuông, hình tròn, chữ nhật hay tam giác của hình học truyền thống Euclid để miêu tả. Trái lại, hình dáng và cấu trúc này lại hoàn toàn tương đồng với nguyên lý tạo hình của các tổ hợp hình học Fractal. Mỗi một tổ hợp hình học Fractal đều có hình thù phức tạp, là tập hợp của vô số mảnh hình học ghép lại. Ngày nay, với sự kết hợp của đồ họa, hình ảnh 3D tạo ra từ thuật toán Fractal có thể mô phỏng được hầu hết mọi cấu trúc phức tạp, bao gồm cả hình thái, cấu trúc dạng đô thị. Hình 3.1 minh họa sự tương đồng giữa ảnh chụp mặt bằng quy hoạch đô thị thực tế với hình ảnh phân nhánh, chia mảnh của lá cây – dạng tự nhiên của hình học Fractal và hình 3.2 minh họa sự tương đồng giữa ảnh chụp mặt bằng quy hoạch chia lô thực tế với hình ảnh ô mảnh tạo ra bằng đồ họa theo các quy tắc tạo hình Fractal.
Đều là các tổ hợp phát triển và biến đổi có tính phân cấp, theo thời gian và không gian
Dưới ảnh hưởng của sự phát triển đô thị và dân số, theo thời gian, hình thái của đô thị biến đổi theo hướng vừa chia nhỏ cấu trúc nội tại, vừa mở rộng hình dạng bao vật lý mà không có hình dạng cố định hay ranh giới cuối cùng. Sự biến đối này đôi khi có thể có những quy luật nhưng cũng hàm chứa rất nhiều đột biến. Đây là đặc điểm mà không một loại hình học nào, ngoại trừ hình học Fractal có. Khu vực đô thị phân chia thành các thửa lớn, giới hạn bởi các tuyến đường giao thông chính. Sau đó, theo thời gian, đường giao thông phân nhánh nhỏ hơn, các ô/ thửa lớn được phân thành các lô/ mảnh nhỏ hơn và quá trình tiếp diễn như vậy theo thời gian, khiến cấu trúc đô thị chia nhỏ dần. Quá trình phát triển cũng tương tự. Trong hình học Fractal, các tổ hợp cũng hình thành từ tổ hợp gốc – gọi là hình phát sinh. Sau đó, tuân theo các quy tắc biến đổi mà có thể mở rộng hay chia nhỏ vào trong theo thứ tự tăng dần. Cứ như vậy, cấu trúc ban đầu trở thành hình phát sinh và nhân bản không ngừng theo quy tắc. Tùy theo loại hình học Fractal mà các quy tắc phát triển có thể hàm chứa đột biến ở một giai đoạn nào đó hoặc bắt nguồn từ một trong các yếu tố khởi tạo hay phát sinh. Vì thế, cũng như hình thái đô thị, các tổ hợp hình học Fractal không có hình dạng cố định mà biến đổi theo thời gian, không gian và có hình dạng không chỉ phức tạp mà còn vô cùng phong phú, tương thích sự phát triển bất quy tắc trong quá trình biến đổi của các hình thái đô thị. Hình 3.3 minh họa sự tương đồng về phát triển hình thái đô thị và tổ hợp hình học Fractal.
Sự đa dạng về hình phân chia hay kết nối
Do các yếu tố văn hóa, xã hội, kinh tế và địa lý tự nhiên giữa các địa điểm khác nhau là khác nhau, nên hình thức thửa – ô – lô – mảnh và cách phân chia hay kết nối trong hình thái đô thị rất phong phú đa dạng. Điều này cũng tương đồng với các tổ hợp hình học Fractal vốn có thể được khởi tạo từ bất của cấu trúc hình học nào và biến đổi, phát triển theo nhiều quy tắc. Hình 3.3 minh họa sự da dạng về cấu trúc chia lô trong hình thái đô thị và cấu trúc ghép/ phân mảnh trong hình học Fractal.
Nhận xét:
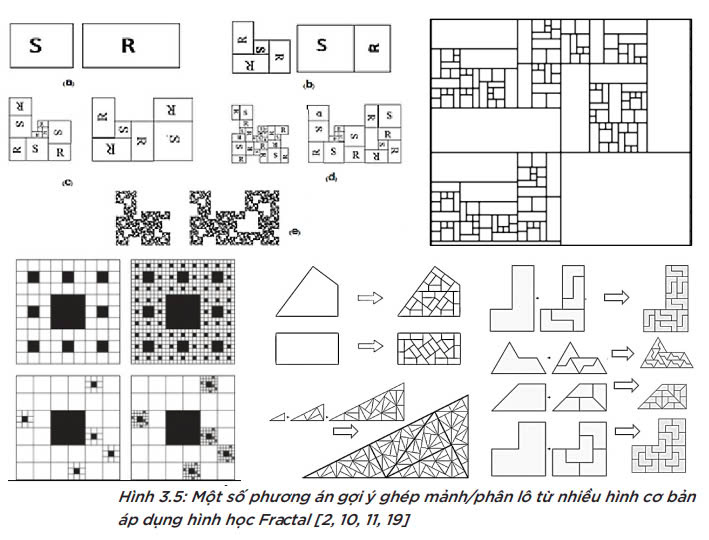
Qua những điểm đã phân tích, có thể thấy, hình học Fractal rất tương thích với tạo hình liên quan tới hình thái đô thị. Chính những sự tương đồng về tạo hình này có thể mở ra nhiều khả năng ứng dụng hình học Fractal trong nghiên cứu hình thái học đô thị, đặc biệt là những quy hoạch dạng phân chia thửa – ô – lô, mảnh. Hiện nay, các nhà nghiên cứu quy hoạch và hình thái đô thị ứng dụng hình học Fractal chủ yếu để mô phỏng hình thái đất đai, mạng lưới đô thị, qua đó đánh giá mức độ tập trung hay khả năng phát triển đô thị thông qua việc tính kích thước Fractal. Tuy vậy, qua phân tích về tạo hình kể trên, hình học Fractal có khả năng ứng dụng như một yếu tố cấu thành khoa học của Hình thức và Cấu trúc đô thị thông qua tiềm năng sáng tạo các kiểu hình thức liên quan tới bản sắc văn hóa của đô thị, được diễn giải dưới dạng các hình thức biểu tượng hoặc nó có thể mô phỏng các không gian đặc trưng của đô thị như một cấu trúc cơ bản có nguồn gốc từ các hoạt động đô thị truyền thống; hay nó có thể biến đổi linh hoạt cấu trúc không gian đô thị nhờ đặc trưng của hình học Fractal. Hình 3.5 minh họa tiềm năng ứng dụng hình học Fractal trong quy hoạch phân chia thửa – ô – lô/ mảnh thông qua sự biến đổi linh hoạt tạo hình phân mảnh.
Kết luận
Tóm lại, hình học Fractal là dạng hình học mới nhất. Với các đặc điểm như gẫy khúc, phức tạp, có khả năng phát triển, biến đổi, các tổ hợp hình học Fractal hết sức phong phú đa dạng, có nhiều điểm tương đồng để miêu tả được hình thái đô thị, đặc biệt là hình thức liên quan đến quy hoạch thửa – ô – lô, mảnh. Hiện nay, ở Việt Nam, việc nghiên cứu và ứng dụng hình học Fractal chưa phổ biến nên rất cần những nghiên cứu sâu để ứng dụng cho từng lĩnh vực cụ thể, trong đó có hình thái học đô thị. Hình học Fractal có thể ứng dụng như một yếu tố cấu thành khoa học của Hình thức và Cấu trúc đô thị. Tuy vậy, cần lưu ý rằng: Các tổ hợp Fractal thì thuần túy là hình học mà sự phát triển hoặc biến đổi hoàn toàn dựa trên những quy luật còn sự phát triển và biến đổi của các dạng hình thái đô thị có nguồn gốc từ các vấn đề văn hóa, xã hội, kinh tế và địa lý của từng vùng, từng dân tộc, từng thời điểm. Nghiên cứu ứng dụng hình học Fractal trong việc mô tả hình thức thửa – ô – lô, mảnh hay hình thái đô thị nói chung cần gắn với các yếu tố đã nêu để tìm ra tổ hợp hình thức và biến đổi sao cho phù hợp nhất có thể.
TS. KTS. Lê Thị Phương Chi
GS.TS.KTS. Doãn Minh Khôi
ThS. Vũ Thu Huyền
Khoa Kiến trúc và Quy hoạch, Trường Đại học Xây dựng Hà Nội
(Bài đăng trên Tạp chí Kiến trúc số 4-2024)
Tài liệu tham khảo
1. Alik, B., Ayyildiz, S. (2016), “Fractals and Fractal Design in Architecture”, Recent, vol 17(3), pp. 282-291
2. Al-Saidi, Nadia, Mohammed, Arkan ( 2012), “A new approach for computing multi-fractal dimension based on escape time method”, International Journal of Mathematical Analysis (Ruse)
3. Amal, O., Lobna, S., Sherif, E. (2014), “Fractal geometry in architecture: from formative idea to superficial skin design”, Conference: Contemporary Discussions and Design Methodologies in Architecture ARCHDESIGN ’14At: İstanbul, Turkey
4. Antonio, C. F., Jose, F. R. Jr., Robson L F Cordeiro, (2016), “Effective and Unsupervised Fractal-Based Feature Selection for Very Large Datasets: Removing Linear and Non-linear Attribute Correlations”, Conference: 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), DOI:10.1109/ICDMW.2016.0093
5. Benoit, M. (1983), Fractal Geometry of Nature, W.H. Freeman and Company, New York.
6. Doãn Minh Khôi (2023), “Hình thái học đô thị”, Nhà xuất bản Xây dựng.
7. Francisco Martínez ,Bastian Sepúlveda, Hermann Manríquez 2,(2013), Land 2023, 12(2), 296; https://doi.org/10.3390/land12020296
8. Hoàng Chúng, Hoàng Quý, Hoàng Tụy (2003), Tìm hiểu Fractal một hình học mới lạ, Nhà xuất bản giáo dục
9. Jean F. G (1996), Physíc and Fractal structures, Springer
10. Jin, Y., Wu, Y., Li, H. et al (2017), “Definition of fractal topography to essential understanding of scale-invariance”. Sci Rep 7, 46672, https://doi.org/10.1038/srep46672
11. Lê Thị Phương Chi (2023), “Ứng dụng hình học Fractal trong thiết kế tổ hợp kiến trúc tại Việt Nam)” – Luận án tiến sĩ , ĐH Xây dựng Hà Nội.
12. Magdy, I., Robert, K. (2004), Generating Fractals Based on Spatial Organization, Illinois Institute of Technology, College of Architecture, Chicago, IL USA
13. Nguyễn Ngọc Hùng Cường (2013), Nghiên cứu về hình học Fractal – viết chương trình cài đặt một số đường và mặt Fractal, Luận án tốt nghiệp Trường ĐH Bách khoa Hà Nội – Trường ĐH Thủy sản Nha Trang, Khoa công nghệ thông tin
14. http://www.fractalcurves.com/Dragon_of_Eve/
15. http://www.fractal-recursions.com/fractals/fractal-01280501v.jpg
16. https://courses.lumenlearning.com/wmopen-mathforliberalarts/chapter/introduction-Fractal-basics/
17. https://fractalfoundation.org/OFC/OFC-12-3.html
18. https://generativelandscapes.wordpress.com/2014/10/07/fractal-trees-basic-l-system-example-9-4/
19. https://www.gettyimages.com/detail/illustration/fractal-pattern-of-rectangles-royalty-free-illustration/1350659169
20. https://www.shutterstock.com/es/image-vector/vector-map-city-florence-italy-692126242
21. https://www.treehugger.com/amazing-Fractals-found-in-nature-4868776